Reimplementing Ruby's Hash

This article is based on my talk at GoGaRuCo 2014.

I got a pretty important phone call a while back.

The President of the United States called me up. I was pretty surprised. He said:

"We've received news of a grave threat. Unless you re-implement Ruby's Hash, alien terrorists will blow up Sea World."

I think he might have said some other stuff, but honestly... I was already typing.

What's a Hash?

You've probably used hashes in Ruby, but what are they? Some languages call them dictionaries or maps. Let's call them "maps", because that's what they do - map a key to a value. So you can say "the key 'appetizer' should have the value 'fruit salad', and then later say "what value does the key 'appetizer' have?" and get back "fruit salad".

#!ruby
map["appetizer"] # => nil
map["appetizer"] =  "fruit salad"
map["appetizer"] # => "fruit salad"

That doesn't sound hard, does it? Nope. We can do this.

Here's an idea: let's make a list of tuples, pairs like [key, value]. For instance:

#!ruby
[["hi", "hola"], ["cat", "gato"]...]

If someone asks for the key "cat", we'll go rummaging through these pairs until we find one where the key is "cat", and we'll return the value "gato". If they want to set "cat" to "chat", we'll find that pair and change "gato" to "chat". If they want to set "dog" to "perro", we'll look through the list, and if we don't find a tuple starting with "dog", we'll make one like ["dog", "perro"] and stick it on the end.

We'll call the class TupleMap. We can even get the nice bracket-bracket syntax, like tuplemap["foo"], because in Ruby, that's just syntactic sugar for method calls like these:

#!ruby
class TupleMap

  # read
  def [](key)
  end

  # write
  def []=(key, value)
  end
end

Seems perfect, right? Well, that's exactly what I did, and it worked. I could insert the key "hokey" with the value "pokey" and get it back out.

#!ruby
t = TupleMap.new
t['hokey']   = 'pokey'
t['hokey']  #=> 'pokey'

Success!

I attached my Ruby class to an email, sent it to the president, and kicked back to relax.

Yay!

Failure

Actually, not "yay". I got another call from the president.

He said: "What kind of Hash is this? A hash is supposed to have O(1) lookup time, and this thing has O(N)."

I said, "I... uh... I'm... I'm sorry Mr. President, I'm having some KKKRRRRSSSHHH hearing you... I think I might have a bad KSSSSHHHHHH, I'll call you ba" [hang up].

I hated to resort to making fake static noises, but I kinda panicked. I was like, "what does O(N) mean, and why does the president know more computer science than I do?!"

If those words sound scary to you, too, take heart! I learned those fancy words, and I have written an extremely friendly explanation, which you should go and read right now.

Really, it's very helpful, you'll totally get it. Go ahead.

Now please get out a marker and sign your monitor on the dotted line below.

I have read Nathan's article on Big O notation, or else I already understand that stuff.

......................................... <-- Your Name Here

Good. Let's continue.

TupleMap's Problem

So what's the problem with TupleMap? We said that if somebody asked for the key "cat", we'd go rummaging through this list, looking for one where the first value is "cat".

[["hi", "hola"], ["cat", "gato"]...]

The problem is that the bigger this haystack gets, the longer it takes to find the needle. If "cat" is in the 100th pair, we'll have to look at 99 non-matching items before we find it; if it's the 1,000th, 999 matching items.

On average, we'll have to look through about 1/2 of the list to find an existing key (either to read or to update it). If we have N items in the list, it will take about 1/2N steps to find it. New keys are even worse: if someone calls hashmap["cow"] = "vaca", we don't know whether that's an update or an insert until we've looked through the entire list; if we didn't find it, it's an insert, and we can add it to the end. That's N steps of checking before we insert - 1,000 steps for a 1,000-item list.

To make this really clear, I wrote a script to test our map class. Basically what I did was this: do some inserts, record how long it took, do some reads, record how long it took, and repeat. At the end, I graphed the data. Here's what it looked like:

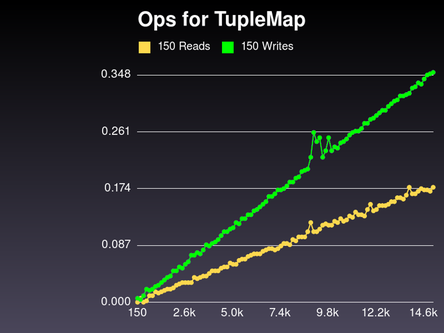
On the X axis, we've got the number of keys in the map, and on the Y axis, how long our reads or writes took. You can see that both reads and writes are basically straight lines with some slope. And if you read my article on Big O analysis, you know that the shape is what we care about, not the exact slope. We can wave away the difference between these two lines because in both cases, the amount of time it takes is proportional to the size of the list. The normal way to say this is that reads and writes are both O(N).

We don't want that. Real hashes, as the President said, should have O(1) read and write times. What can we use that's O(1)?

Array lookup by index

One thing we know of that's O(1) is array lookup by index. some_array[328] is just as fast as some_array[5]. But why is that?

First, because it's looking in RAM. RAM is "random access memory", which means that you can access any randomly-chosen part of it just as quickly as any other. That's in contrast to a spinning disk; on a spinning disk drive, if you were reading from one part of the disk and wanted to get data from from another part, you'd need to spin the disk around and move the read head to the new location, which takes a bit of time. Far-away data would take longer to access than nearby data.

But with RAM, we don't have to run from one part of a disk to another - we can teleport. As long as we know the location of what we want in RAM, we can go straight there and get it.

So how do Ruby's arrays use that? Well, Ruby knows where in RAM an array starts. It also knows that each slot in the array contains a pointer to an item (not the item itself), and each pointer is the same number of bytes "wide" as the previous one. So when you ask for the 5th item, you can imagine Ruby saying, "The array starts at address 100 in RAM, so the 5th item is at address 105". Then it goes straight there in RAM and gets it.

How can we use that?

OK, we know that array lookup by index is O(1). How can we use that to build a map that's O(1), too?

We'll use what's called a "hash table" - the underlying data structure that gives the Ruby Hash class its name. We'll call our new class HashMap.

The basic idea has two parts.

HashMap Part 1: A digest function

We know a fast way to look up numeric keys: namely, arrays. We want a fast way to look up string keys. So logically, we need a way to convert strings to numbers. Something like this:

index_of("appetizer") => 2

You might see this called a "hash function", but that can be a bit confusing - we've got a hash function to use in a hash table to build our Hash class.

Ruby actually makes this easier by using the term "digest function", which is a great description, because just like digestion, it's a one-way process. You can turn pizza into poo, but you can't turn poo back into pizza.

(At least, not the same pizza.)

We need two things from our digest function: 1) turn the key into a number and 2) always give the same number back for the same key. In other words, if index_of("appetizer") is 2 the first time, it had better be 2 every time we call it.

The reason it needs to be predictable is because of...

HashMap Part 2: A sparse array

We'll start with an array of nils:

[nil, nil, nil, nil, nil...]

...and if we want to store the value "fruit salad" for the key "appetizer", we'll use our digest function to decide where to put it.

#!ruby
index = index_of("appetizer") # => 2
array[index] = "fruit salad"
array # => [nil, nil, "fruit salad", nil, nil...]

Now you can see why the digest function must be predictable. If someone inserts "appetizer", and we compute a digest of 2 to store it, we want to be sure that we will look in slot 2 to find it later when they ask for the same key.

I called this a "sparse" array because it starts out with a bunch of nils. That's because if we know our digest might return a value as high as 99, we'd better have a slot 99 to put something in, and the only way to have that is to have slots 0-98 existing and empty.

OK! So with this strategy, we'll be able to compute the digest of a key and go instantly to the slot where its value should be stored, either to lookup or to write. That's O(1) on both counts. Success! Right?

...Right?

Problems

Oh, of course there are problems. There are always more problems! That's why we never run out of work, we programmers. Our problems have problems. Our solutions have problems! Back to work.

Problem 1: Collisions

The first problem is collisions. We want to use the digest value of a key to decide where to put it in our array. But what if we get multiple keys with the same digest value? That's a "collision".

#!ruby
index_of('appetizer') # => 2
index_of('mammal'  )  # => 2 - D'oh!

What do we put at index 2?

We can solve this problem by using "buckets" - put both values in slot two, along with their respective keys.

#!ruby
[
  nil,
  nil,
  # Tuples again!
  [
    ['appetizer', 'fruit salad'],
    ['mammal',    'water buffalo']
  ],
  nil...
]

Then when somebody asks for the key "mammal", we hash it, go to the right slot, find a bucket, rummage through it until we find a tuple with the key "mammal", and return the value.

That works, but if we let those buckets grow unchecked, we'll be right back where we started: the more items we have, the longer it will take to find anything. We'll have to limit the size of those buckets somehow. We'll get back to that.

Meanwhile, we have another problem.

Problem 2: Waste

#!ruby
[
  nil,       # waste
  nil,       # waste
  (a bucket),
  nil,       # waste
  nil...     # waste
]

Look at all those nils! They're there for a reason: our next key might go in slot 4 or slot 204 (depending on how big a number our digest function can generate), and we need to be ready for that. But isn't that a waste of memory?

Yes, but in this case, the solution is: get over it.

This is a fundamental tradeoff that hashes make. We're willing to waste some memory so that we get O(1) access times. You can be memory-efficient, like TupleMap, but spend a lot of time rummaging around for the key you want, or you can be time-efficient, like HashMap, but waste some memory on blank spaces. That's the choice.

(Incidentally, the real Ruby Hash class has it both ways: if you make a tiny hash, with 2-3 keys, it's like TupleMap internally; if you make it big enough, it converts to something like HashMap to maintain performance.)

Is there an optimal solution? A great solution here would:

• Minimize collisions (which hurt our access times)
• Minimize wasted memory

Yes, there's a way to do that.

Big Idea: Start Small, Grow as Needed

To optimize our memory/speed tradeoff, we'll start out with a small number of slots/buckets, so that we're not wasting much memory. As we get more keys, anytime we see that we've got too many collisions, we'll make more buckets and redistribute our keys among them - use a bit more memory, keep our speed.

Now, we have to be careful about how we redistribute. It won't help us to have 100 buckets if we still have to rummage through a few full ones for most of our keys. We want to spread our keys out.

Old Buckets    New Buckets - failure    New Buckets - success

|--            |---                     |-
|--            |--                      |
|---           |---                     |-
|-             |                        |-
               |                        |--
               |                        |
               |                        |-
               |                        |-
               |                        |
               |                        |-

And when do we redistribute? "Too many" collisions is a bit subjective, so to make it concrete, let's say "we don't allow more than 10 keys per bucket." (A fixed limit means that looking through any given bucket will not take more than 10 steps, whether the overall map has 10 keys or 10 million, so we can call that O(1).)

Making a Plan

Here's what we'll do.

1. We'll start with an arbitrary number of buckets - say, 10
2. When we want to access a key, we'll first compute its "raw digest value" (a number). More details on that later.
3. That raw digest might be 1,392,279, but we might only have 10 buckets. So to map that to a bucket we actually have, we'll say bucket_number = raw_digest_value % number_of_buckets

You probably know what modulo means, but just in case you don't, it's basically "divide and take the remainder." Eg:

Value  | modulo 10
10     | 0
11     | 1
22     | 2
101    | 1
1,000  | 0

If we have 3 buckets, any raw digest % 3 will map to one of our valid index values: 0, 1, or 2.

Raw digest value | index
------------------------
3                | 0
7                | 1
10               | 1
309406           | 1
-9384292039948   | 2

When we grow, we'll be going from some number of buckets to some other number of buckets, and the whole point is to spread out the keys. If we grew from 3 buckets to 6 buckets, we wouldn't spread things out well, because a lot of numbers that divide evenly by 3 also divide evenly by 6. That means a lot of the keys that were in slot 0 will still be in slot 0. Not good.

But suppose we grow from 3 slots to 7. For most numbers, x % 7 will be different from x % 3.

Raw digest value |% 3|% 7 
------------------------------
3                | 0 | 3
7                | 1 | 0
10               | 1 | 3
309406           | 1 | 6
-9384292039947   | 2 | 1

That would be a good way to grow - we'd spread our keys out nicely. So how can we generalize that - if we're at a particular size, what size should we grow to?

One strategy that works well is this: double the size, then find the next prime. Eg, 199 slots, then 401, then 809, 1619, 3251, 6521, etc.

The fact that each number is prime means we'll spread things out nicely. And the fact that we (roughly) double in size means that we don't have to do this very often.

That's important because every time we grow, we have to "rehash" - we have to calculate a new digest for every single key. That's an O(N) operation - the more keys we have, the more steps it takes.

That's OK - it's just the nature of the problem. But we don't want to do it often. If we grew from 10 to 11, then from 11 to 12, etc, we'd be rehashing constantly. But if we double the size each time, we won't have to rehash more than a time or two in most cases.

What about that Raw Digest?

We said we'd compute a raw digest value for every key, then modulo it, blah blah blah. But how do we compute the raw digest? How do we turn our key into a number?

#!ruby
def raw_digest(key)
  # ??
end

My first thought was: I can take a string key, turn it into Unicode codepoints (which are numbers), smash those together, and call them the raw digest.

#!ruby
"blam".codepoints # => [98, 108, 97, 109]
"blam".codepoints.join.to_i # => 9810897109

That works for strings, but we have to support more than strings. In Ruby, anything can be a hash key - a string, a symbol, an array, a UserDecoratorSubscriberFactory - anything.

So our first requirement for our digest function is it must work with all Ruby objects.

#!ruby
# all must work
hash['a']
hash[['a', 'e']]
hash[Hat.first]

OK, well, every object has an object_id, right? And that's a number. Can we use that?

#!ruby
"lemur".object_id => 70150729361440
%w[hay fever].object_id => 70150741120160

Well, it's a number, yes. But it won't support this totally normal usage of a hash:

#!ruby
hash["fruit"]   = "apple"
hash["fruit"] #=> "apple"

That's because the string "fruit" on the first line is an object, and the string "fruit" on the second line is a different object. It will have a different object id, map to a different bucket, and won't find the value inserted with the first string.

That stinks. We don't care that those two strings are different objects; they're the "same value". And that's our second requirement: "same value" keys need to be interchangeable as keys in our hash.

But that's a subjective concept, isn't it? Suppose we use a Hat object as a key. What makes another Hat have the "same value" as the first one? Same size? Same color? How will we know what to return here?

#!ruby
a, b = HatCollection.take(2)
hash[a]  = 'something'
hash[b] #=> ??

Ruby has a sensible way of answering this question. To get the hash value of an object, ask the object. Every object supports the .hash method, so every object can decide what has the "same value" as it.

#!ruby
some_hat.hash   #=> 56268189660135834
'hi'.hash       #=> 1426215061227324254
['a', 'b'].hash #=> -1590378560689017266 

If you want to use your Hat class as a hash key, and you want two hats of the same size to be interchangeable as hash keys, you can define .hash such that it depends only on the size. The only catch is that its sister method, .eql?, needs to agree. In other words, if hat1.hash == hat2.hash, make sure that that hat1.eql?(hat2). That's because .hash is used to find the right bucket, and .eql? is used to find the right tuple in that bucket.

Review

OK, so here's how our fancy new homegrown hash works.

1. We make a sparse array of buckets of key-value tuples. Eg: [nil, nil, [["appetizer", "fruit salad"]], nil...]
2. For any key, key.hash % number_of_buckets tells us which bucket it goes in.
3. For any tuple in that bucket, key.eql?(bucket[0]) tells us whether it's the key we're looking for
4. Whenever any bucket gets 10 keys, we make more buckets (double the current number + a little bit to find a prime). We re-digest all our keys and spread them out. This increases our memory usage, but maintains our fast access times.

So: does it work?

Did We Achieve O(1)?

If we've achieved O(1) performance, it would mean that we can insert or look up a key in the same amount of time, regardless of whether the hash has 10 keys or 10,000. We should be able to graph the read and write time for ever-larger hashes and see a flat line. So... drum roll, please!

...

Bam!

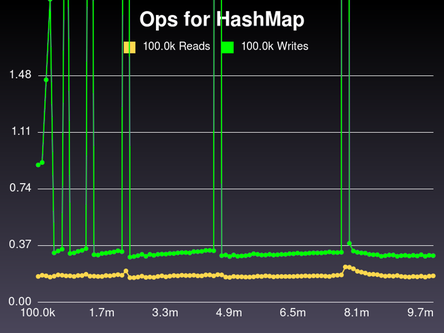
Oh... hmmm. OK, don't panic. It's not as bad as it looks.

First off, notice that most of the operations actually fall onto two flat lines. Here, I'll trace them in red.

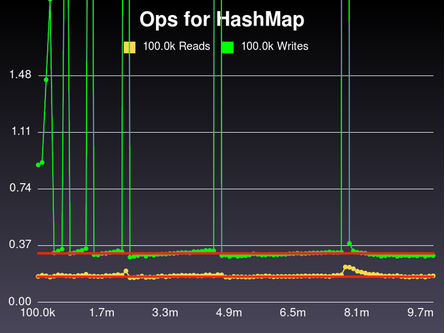
See? A bunch of reads when there are 9.7 million keys is no slower than if there are only 10k. And the writes work the same way... mostly.

But what's up with the spikes? Well, those spikes happen when we redistribute keys. Our buckets fill up, we make more, we re-digest every key, and we spread things out. We expected those spikes. In fact, the native Ruby hash has similar spikes as it grows.

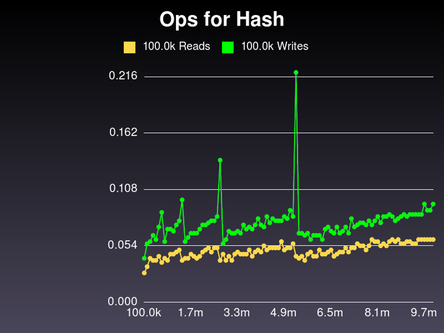
Of course, Hash takes about 2/10th of a second to re-digest about 5 million keys. How long does our implementation take?

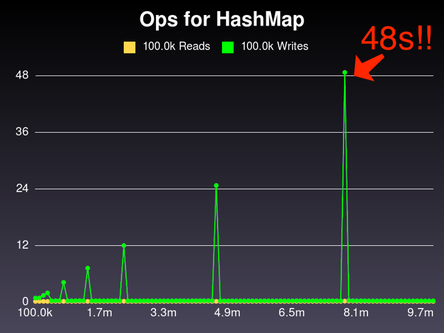
Oh! Our spike at 8.1 million keys takes 48 seconds.

That's pretty terrible. Don't use this hash in production, folks.

But have we failed? Is this hash incorrect?

Surprisingly, no! Let's look at this hash side-by-side with Ruby's.

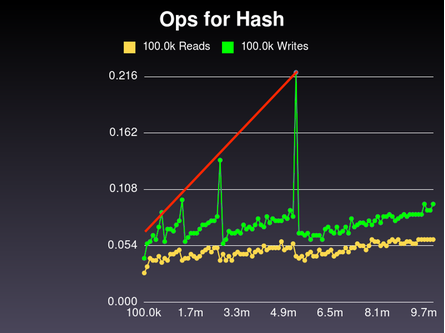
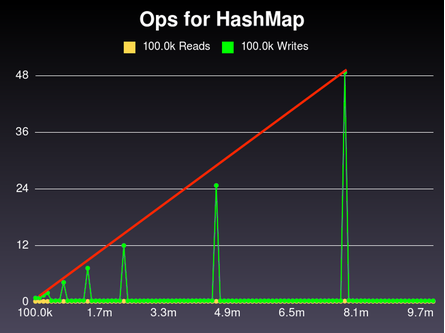
Notice that both of them have spikes of linearly-increasing size. That makes sense - the number of keys to re-digest keeps getting larger. The slope on the Ruby hash isn't nearly as steep as ours, but it's still linear growth.

And we actually do get O(1) performance for reads and writes. Lemme 'splain it to you.

• Reads are always <= 10 steps, because we never have more than 10 keys per bucket.
• Writes are the same, unless the write happens to trigger a redistribution
• As our redistributions get more expensive, they also get less frequent (remember, we double each time). If you squash each peak into the valley to its left, you get a level landscape; the average write speed stays the same. So we can say that using an "amortized analysis", our writes are O(1) - with each write, we incur a little debt, and occasionally we pay it off, but the average debt per write stays constant.

So: yay!! And furthermore: wooo!

When I reached this conclusion, I emailed my fancy HashMap to the president and patted myself on the back for a well-completed mission.

Then I pondered: could we, should we make it faster?

Optimizations?

We could. We could implement the whole thing in C, like Ruby does. Or we could re-digest concurrently (sounds hard). Or we could experiment with how much we grow at a time. We could probably improve it.

But honestly, why bother? Ruby's native hash is really great.

What Else Can we Learn?

For one thing, hashes are amazing, high-performance multi-tools. There are lots of programming challenges where the answer is basically "use a hash".

We can also apply these lessons to the hashes that call themselves "databases" - the "distributed hash table" ones like Riak, Cassandra, or anything based on Dynamo DB. They use a digest function to decide where in a cluster of servers to store your data.

And they have the same trade-offs as an in-memory hash. For instance, to grow your cluster, you need to re-hash every key and decide which node it should live on now. If you're going to all that trouble, don't add one node - add a lot. Double your nodes, maybe, so you don't have to repeat the process for a while.

I was pondering over these things, stroking my beard and smoking my bubble pipe, when I got another phone call.

Uh Oh

The president called me back and said "Dude! Where's your hash?"

I said, "What are you talking about, Mr. President? I sent you that email three hours ago."

He said "I never got an email from you."

I looked in my email account, and there it was, sitting in my outbox! I said, "I'm sorry, Mr. President, I thought I sent it, I'll send it right now."

He said "It's too late. Alien terrorists blew up Sea World."

Noooooooo!

Oh! Whew. It was just a dream.

Thanks for reading.

Postscript

You're still here? Wow, you are one determined reader!

If you're still hungry for more, you can see my implementations of TupleMap and HashMap, or maybe look at how Rubinius implements Ruby's Hash. You can also read some CS lecture notes on hash tables and amortized analysis.